振动波的特性简述
[下载原文PDF]
对于超声传感器，小编一直有一个想法，想对该传感器的基本特性——波，写点什么作为基本的说明。超声传感器中有一类和振动传感器核心件相似，多为压电材料，但是作用却不尽相同：
- 振动传感器内的压电晶体是通过振动挤压而生电信号，通过电信号检测振动状态；
- 超声传感器如果则可分为发射型、接收型和收发型超声换能器。发射型追求的是输出功率和转换效率；接收型要的是宽的频带和高的灵敏度；收发型则最好二者兼而有之。
振动传感器所检测的振动信号其频率可以是在人的听觉范围之内，也可以在听觉范围之外（频段处于超声或者次声），而超声波则强调并利用了超声波的特性。不管波的形式如何，我们还是喜欢就繁从简的方式，来处理分析问题。比如，通过基频或谐波来剖析信号，因为将基频和谐波最终合成就可以恢复波的原形，更不要说很多时候我们谈到波就想到正弦或者余弦的周期重复形态了。本文对波的一般特性的导出进行了整理。
波的一般抽象描述[1]
直接上x轴向的纵波（质点运动方向平行于波的传播方向）：
，c为常数，t为时间 （1）
取其中的
，当
时，
，方程
表示在T=
时波的形态。
如果在
时刻在轴的
位置处取值，我们又可以得到原来的波形函数 
，相当于将波形在
时间内维持不变地左移了
。可以理解为：如果将波沿x轴在
时间内向左移动
的距离，则和t时刻原x处的波形一致。这说明该部分纵波函数是沿着x轴左向以速度c传播的。
同理可以这样理解
。只是传播方向和前面相反。
该函数还有一个特点。如果我们对函数
分别对x和t进行求二次偏导，令
，
，可得：
即：
（2）
事实上，公式（1）是函数（2）的通解形式，而且无论纵波还是横波（质点运动方向垂直于波的传播方向），理想情况下，波动方程的形式就如（2）所示。
波动方程的栗子（1）——弹性绳索的横波振动
图-1 弹性绳索的振动
为方便示意个参数，将振动画成了振“荡”。实际的理论推导时，要求振动幅度要小得多。图-1中，设平衡位置处的均匀弹性绳索的张力处处为T，均质，线密度为
，绳索只有y方向的上下振动，没有x水平方向的运动，则取x处的很小长度为
的绳索受力分析如下：
水平方向：
，当
趋于极小时，
，
垂直方向：
，当振动幅度趋于很小时，
，
，所以有：
当
趋于极小时，上式有：
因为
，所以上式有：
上式的左侧由拉格朗日中值定理得：
，
，从而得： 
，令
，则：
。
大家根据式（2）知道公式中的各项所指，张力T越大（弦绷得越紧），线越轻细，波速越快，与我们体验上也是一致的。
波动方程的栗子（2）——3维弹性体的等容波（弹性体的任一部分体积应变为0）[1]
弹性体中任一点的位移分量用
表示，我们直接给出运动微分方程：
（3）
同时还有一个弹性应力应变方程：
（4）
其中
为正应力，
为切应力，
为体力，
为密度， 
为体积应变，
是弹性模量，
为泊松比。体积应变为：
记
，在等容位移设定下，
。
将式（4）代入（3），忽略体力
，再将
=0代入该中间结果得等容波动方程：
（5）
其中，
，表示波速。等容波是弹性波的基本形式之一。
波动方程的栗子（3）——切向极化薄圆环压电陶瓷扭转振动[2]
兜兜转转终于到了和超声振动相关的部分了。
前面的栗子都是纯机械振动，但是超声传感器，比如压电体，则在受压过程中在表面产生电压电荷，或者在施加振荡电信号之后会产生振动，是某种意义上的“机电一体化”。由于压电效应和逆压电效应，压电材料中的机械能和电能之间会产生相互耦合和转换，这就是压电材料中提到的机电耦合系数及机电转换系数来描述的。
图-2 切向极化薄圆环扭振
在图-2中所示，圆环的半径a远大于厚度，且厚度与剪切波波长可比拟相近，P为振子的极化方向，工作时的外加电场
沿z轴方向，所以圆环只有沿z轴的扭转，即
，而其他应变分量都为0，并且振子材料绝缘，忽略边缘效应，电位移参数中，
，而
，
。于是有以下的应变和压电方程组：
（6）
其中，
表示切向应力和应变矩阵，
是电位移和电场强度（轴向）矩阵，
为 恒电位移下的弹性刚度常数矩阵，
是压电劲度常数矩阵，
为恒应变下的介电隔离率矩阵。
和式（4）类似的应力应变方程组相比，式（6）中多出了由于电场电位移引起的应力变化部分。令
为剪切振动的扭转角，在薄圆片的条件下，扭转角和切应变的关系为：
，（r为振子中任一点半径） （7）
压电振子的分析处理要结合压电方程、力学方程以及力学电学的边界条件进行综合推导。对于上面的振子模型，如果取z轴方向的任意一个截面s，在运动力学方面有，该截面处的扭矩M：
（8）
将式（6），（7）代入式（8）后得：
（9）
取振子内厚度为
的任一微分单元环，该微分单元的力矩平衡方程有：
（10）
因为设定
，所以根据式（9）和（10），得：
（11）
很显然，式（11）依旧是一个波动方程。波速是
。
在这个栗子中，决定弹性波传播速度的包括了受压电效应反作用下的弹性刚度系数
，因此在该模型中，波的振动模式确实是受压电常数影响的。
如果要求解该薄环的谐振频率等参数，还需要联列振子的电路状态方程，考虑机电转换系数，然后才有振子的机电特性的解算，并据此计算振子的谐振频率。超声换能器多工作在共振频率处才可以具有较好的转换效率。如果知道了波速，有了谐振频率，那么就知道工作最佳波长，就可以设计外围的驱动或者接收电路，以及阻抗匹配的要求。
以上仅仅是超声换能器设计中涉及到的某个环节。还有其他方面的考量吗？
超声换能器的设计步骤和考虑
设计传感器的首先是确定设备在其使用寿命期间工作温度范围。重要的是要考虑预期的最大瞬态温度和持续的长期使用温度。因为温度限制了可使用压电材料的选型。
其次，是考虑应用和具体要求。该设备是用作探伤仪还是流量计？它需要绝对灵敏度还是需要高功率输出？用最一般的术语来说，它是在一发一收模式中使用还是作为脉冲回波器件使用？这些问题的答案也限制了陶瓷的选择，并有助于定义性能要求。大多数性能要求，特别是在设计过程的初始阶段，是作为目标而不是规格。重要的是不要指定任何非绝对需要的东西，直到必须需要指定参数为止。如果在最关键的时刻人为地限制了设计过程，可能使设计最终无法进行。
随后，是考虑其他环境要求，如压力，化学品暴露，磁场等。其中一些选项也可以作为设计目标，但通常它们是由最终用途决定的。
接下来，需要考虑任何物理约束，例如尺寸或重量。这些通常也由应用决定，但有时也是设计目标（如：尽可能小巧）。
最后，需要迭代该设计过程，以权衡实际情况和设想的设计目标。例如，阻尼设计可能受到背衬材料可用空间的限制。很多时候，经过权衡利弊会迫使人们考虑新的方法或想法。
当然，还有更加简单的解决方案。安费诺传感器旗下的Piezo Technologies可以依据已有的丰富应用储备，为我们用户提供从设计到生产的完整服务。
以下算是题外话，请不必在意多读一段，了解一下虚无如今却无所不在的电磁波。
从麦克斯韦方程到波动方程[3]
（a）
麦克斯韦方程组的微分形式。式（a）中分别描述：
- 变化的磁场
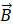可以产生电场
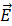； - 自由电荷
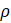可以产生感应电场
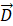； - 传导电流
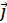和变化的电场
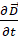可以产生磁场
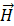； - 磁场
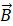是闭合的，无自由磁荷。
其中，
，
，
。其中，
为电导率；
为介电常数；
为介质磁导率。
是哈密顿算子：
。在真空中，有：
，同时传导电流
对
两边取旋度，得：
- 左侧
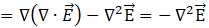
- 右侧
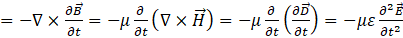
所以：
，即
，其中
，这里的
为已知真空介电常数；
为已知真空介质磁导率。很巧，结果C等于光速。
所以说，自然会联想到光也是电磁波啊。这是电场部分的。同理可以推导出来磁场部分的波动方程：
。事实上，二者不可独立，所以：
以上的所有波动方程，和具体的波的振型还有不少差别。实际计算过程中，需要补充相应的边界条件以及外部输入等才可以解算各个部分的未知量，或者让未知数转换为常量。
[1] 徐芝纶. 弹性力学. 第5版. 高等教育出版社. 2016. 3
[2] 林玉书. 超声换能器的原理和设计. 科学出版社. 2004.6
[3] Daniel Fleisch. 麦克斯韦方程直观. 机械工业出版社. 2014.7
